Exercise 6.2

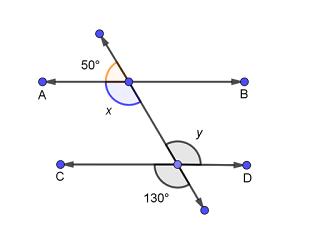
Q1. In the given figure, find the values of x and y and then show that AB ‖ CD.

Given: Figure

To prove: AB ‖ CD

Proof: 50° + x = 180° (Linear pair)

⇒ x = 180° – 50° = 130°

Now, y = 130° (Vertically opposite angles)

∴ x = y = 130°

But they are alternate interior angles

∴ AB ‖ CD

Q2. In the given figure, if AB ‖ CD, CD ‖ EF and y:z = 3:7, find x.

Given: AB ‖ CD, CD ‖ EF and y:z = 3:7

To find: x

Solution: Let y = 3a and z = 7a

AB ‖ CD and CD ‖ EF [Given]

AB EF

x = z = 7a (Alternate interior angles)

Now, x + y = 180° (Co-interior angles)

7a +3a = 180°

10a = 180°

a = 18°

x = z = 7a = 7 x 18° = 126° Ans.

Q3. In the given figure, if AB ‖ CD, EF ⊥ CD and ∠GEF = 126°, find ∠AGE, ∠GEF and ∠FGE.

Given: AB ‖ CD, EF ⊥CD and ∠GEF = 126°

To find: ∠AGE, ∠GEF and ∠FGE

Solution: AB ‖ CD (Given)

∴ ∠AGE = ∠GED = 126° Ans. (Alternate interior angles)

∠GEF = ∠GED – 90° = 126° – 90° = 36° Ans.

Now, ∠FGE + ∠GED = 180° (Co-interior angles)

∴ ∠FGE = 180° – 126° = 54° Ans.

Q4. In the given figure, If PQ ‖ ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.

Given: PQ ‖ ST, ∠PQR = 110° and ∠RST = 130°

To find: ∠QRS

Construction: Draw a line AB ‖ ST through point R

Solution: PQ ‖ ST and AB ‖ ST (Given)

∴ PQ ‖ AB

∠PQR + ∠QRA = 180° (Co-interior angles)

⇒ 110° + ∠QRA = 180°

⇒ ∠QRA = 180° – 110°

⇒ ∠QRA = 70°

Now, ∠RST + ∠SRB = 180° (Co-interior angles)

⇒ 130° + ∠SRB = 180°

⇒ ∠SRB = 180° – 30°

⇒ ∠SRB = 50°

Now, ∠QRA + ∠QRS + ∠SRB = 180° (AB is a straight line)

⇒ 70° + ∠QRS + 50° = 180°

⇒ 120° + ∠QRS + 50° = 180°

⇒ ∠QRS = 180° – 120° = 60° Ans.

Q4. In the given figure, if AB ‖ CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Given: AB ‖ CD, ∠APQ = 50° and ∠PRD = 127°

To find: x and y

Solution: ∠APQ = ∠PQR (Alternate interior angles)

∴ x = 50° Ans.

Now, ∠PRQ + 127° = 180° (Linear pair)

⇒ ∠PRQ = 180° - 27° = 53°

Now, x + y + ∠PRQ = 180° (Angle sum property of a triangle)

⇒ 50° + y + 53° = 180°

⇒ 103° + y = 180°

⇒ y = 180° – 103° = 77° Ans.

Q6. In the given figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ‖ CD.

Given: PQ and RS are two mirrors placed parallel to each other

To prove: AB ‖ CD

Construction: Draw BX ⊥ PQ and CY ⊥ RS

Proof: ∠ABX = ∠CBX and ∠DCY = ∠BCY [Angle of incidence = Angle of reflection]

But ∠CBX = ∠BCY (1) (Alternate interior angles)

∴ ∠ABX = ∠DCY (2)

Adding (1) and (2), we get

∠CBX + ∠ABX = ∠BCY + ∠DCY

⇒ ∠ABC = ∠DCB

But they are alternate interior angles

∴ AB ‖ BC

Exercise 6.1

Q1. In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.

Given: Lines AB and CD intersect at O.  

To find: ∠BOE and reflex ∠COE

Solution: ∠AOC = ∠BOD = 40° (Vertically opposite angles)

But ∠AOC + ∠BOE = 70° (Given)

∴ ∠BOE = 70° – 40°

= 30° Ans.

Now, ∠AOC + ∠COE + ∠BOE = 180° (AB is a straight line)

∴ 40° + ∠COE + 30° = 180°

⇒ 70° + ∠COE = 180°

⇒ ∠COE = 180° – 70°

⇒ ∠COE = 110°

∴ Reflex ∠COE = 360° – 110° = 250° Ans.

Q2. In the given figure, lines XY and MN intersect at O. If ∠POY = 90° and a:b = 2:3, find c.

Given: Lines XY and MN intersect at O. ∠POY = 90° and a:b = 2:3.

To find: c

Solution: Let a = 2x and b = 3x

∠POY = 90° (Given)

∴ ∠POX = 90° (Linear pair)

⇒ a + b = 90°

⇒ 2x + 3x = 90°

⇒ 5x = 90°

⇒ x = 18°

∴ a = 2x = 36° and b = 3x = 54°

Now, b + c = 180° (Linear pair)

⇒ 54° + c = 180°

⇒ c = 180° – 54°

⇒ c = 126° Ans.

Q3. In the given figure, if ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.

Given: ∠PQR = ∠PRQ

To prove: ∠PQS = ∠PRT

Proof: ∠PQS + ∠PQR = 180° (1) (Linear pair)

∠PRT + ∠PRQ = 180° (2) (Linear pair)

From (1) and (2), we get

∠PQS + ∠PQR = ∠PRT + ∠PRQ

But ∠PQR = ∠PRQ (Given)

∴ ∠PQS = ∠PRT 

Q4. In the given figure, if x + y = w + z, then prove that AOB is a line.

Given: x + y = w + z

To prove: AOB is a line

Proof: x + y + z + w = 360° (Complete angle)

But x + y = w + z (Given)

∴ x + y + x + y = 360°

⇒ 2x + 2y = 360°

⇒ 2 (x + y) = 360°

⇒ x + y = 180°

∴ AOB is a line

Q5. In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = ½ (∠QOS – ∠POS).

Given: POQ is a line. Ray OR line PQ. OS is another ray lying between rays OP and OR.

To prove: ∠ROS = ½ (∠QOS – ∠POS)

Proof: OR ⊥ PQ (Given)

∴∠POR = 90°

∠POS + ∠ROS = 90° (1)

and ∠POS + ∠QOS = 180° [Linear pair]

⇒ (∠POS + ∠QOS)/2 = 180°/2

⇒ ½ ∠POS + ½ ∠QOS = 90° (2)

From (1) and (2), we get

∠POS + ∠ROS = ½ ∠POS + ½ ∠QOS

⇒ ∠ROS = ½ ∠POS + ½ ∠QOS – ∠POS

⇒ ∠ROS = ½ ∠QOS – ½ ∠POS

⇒ ∠ROS = ½ (∠QOS – ∠POS)

Q6. It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.

Given: ∠XYZ = 64° and XY is produced to point P. Ray YQ bisects ∠ZYP.

To find: ∠XYQ and reflex ∠QYP

Solution: ∠XYZ + ∠ZYP = 180° (Linear pair)

∴ ∠ZYP = 180° – ∠XYZ = 180° – 64° = 116°

∠ZYQ = ½ ∠ZYP = ½ (116°) = 58°

∠XYQ = ∠XYZ + ∠ZYQ = 64° + 58° = 122° Ans.

∠QYP = ∠ZYQ = 58°

∴ Reflex ∠QYP = 360° – 58° = 302° Ans.