Exercise 6.2

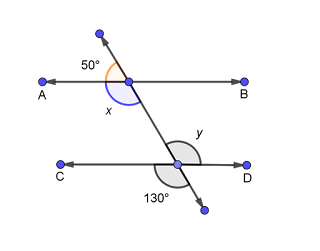
Q1. In the given figure, find the values of x and y and then show that AB ‖ CD.

Given: Figure

To prove: AB ‖ CD

Proof: 50° + x = 180° (Linear pair)

⇒ x = 180° – 50° = 130°

Now, y = 130° (Vertically opposite angles)

∴ x = y = 130°

But they are alternate interior angles

∴ AB ‖ CD

Q2. In the given figure, if AB ‖ CD, CD ‖ EF and y:z = 3:7, find x.

Given: AB ‖ CD, CD ‖ EF and y:z = 3:7

To find: x

Solution: Let y = 3a and z = 7a

AB ‖ CD and CD ‖ EF [Given]

AB EF

x = z = 7a (Alternate interior angles)

Now, x + y = 180° (Co-interior angles)

7a +3a = 180°

10a = 180°

a = 18°

x = z = 7a = 7 x 18° = 126° Ans.

Q3. In the given figure, if AB ‖ CD, EF ⊥ CD and ∠GEF = 126°, find ∠AGE, ∠GEF and ∠FGE.

Given: AB ‖ CD, EF ⊥CD and ∠GEF = 126°

To find: ∠AGE, ∠GEF and ∠FGE

Solution: AB ‖ CD (Given)

∴ ∠AGE = ∠GED = 126° Ans. (Alternate interior angles)

∠GEF = ∠GED – 90° = 126° – 90° = 36° Ans.

Now, ∠FGE + ∠GED = 180° (Co-interior angles)

∴ ∠FGE = 180° – 126° = 54° Ans.

Q4. In the given figure, If PQ ‖ ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.

Given: PQ ‖ ST, ∠PQR = 110° and ∠RST = 130°

To find: ∠QRS

Construction: Draw a line AB ‖ ST through point R

Solution: PQ ‖ ST and AB ‖ ST (Given)

∴ PQ ‖ AB

∠PQR + ∠QRA = 180° (Co-interior angles)

⇒ 110° + ∠QRA = 180°

⇒ ∠QRA = 180° – 110°

⇒ ∠QRA = 70°

Now, ∠RST + ∠SRB = 180° (Co-interior angles)

⇒ 130° + ∠SRB = 180°

⇒ ∠SRB = 180° – 30°

⇒ ∠SRB = 50°

Now, ∠QRA + ∠QRS + ∠SRB = 180° (AB is a straight line)

⇒ 70° + ∠QRS + 50° = 180°

⇒ 120° + ∠QRS + 50° = 180°

⇒ ∠QRS = 180° – 120° = 60° Ans.

Q4. In the given figure, if AB ‖ CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

Given: AB ‖ CD, ∠APQ = 50° and ∠PRD = 127°

To find: x and y

Solution: ∠APQ = ∠PQR (Alternate interior angles)

∴ x = 50° Ans.

Now, ∠PRQ + 127° = 180° (Linear pair)

⇒ ∠PRQ = 180° - 27° = 53°

Now, x + y + ∠PRQ = 180° (Angle sum property of a triangle)

⇒ 50° + y + 53° = 180°

⇒ 103° + y = 180°

⇒ y = 180° – 103° = 77° Ans.

Q6. In the given figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB ‖ CD.

Given: PQ and RS are two mirrors placed parallel to each other

To prove: AB ‖ CD

Construction: Draw BX ⊥ PQ and CY ⊥ RS

Proof: ∠ABX = ∠CBX and ∠DCY = ∠BCY [Angle of incidence = Angle of reflection]

But ∠CBX = ∠BCY (1) (Alternate interior angles)

∴ ∠ABX = ∠DCY (2)

Adding (1) and (2), we get

∠CBX + ∠ABX = ∠BCY + ∠DCY

⇒ ∠ABC = ∠DCB

But they are alternate interior angles

∴ AB ‖ BC